Giải thuật Prim: tìm cây khung nhỏ nhất

Giải thuật Prim là gì ?

Giải thuật Prim, cũng giống như giải thuật Kruskal, là để tìm cây khung nhỏ nhất dựa vào giải thuật Tham lam.

Giải thuật Prim, trái ngược với giải thuật Kruskal, xem các nút như là một cây riêng là và vẫn cữ tiếp tục việc thêm các nút mới vào cây khung từ đồ thị đã cho. Giải thuật Prim phụ thuộc vào điểm bắt đầu.

Để so sánh với giải thuật Kruskal và để hiểu giải thuật Prim sâu hơn, chúng ta sẽ sử dụng cùng một ví du như trong giải thuật Kruskal:

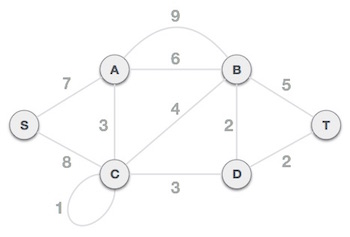
Bước 1: Xóa các vòng và các cạnh song song

Xóa tất cả các vòng và các cạnh song song từ đồ thị đã cho. Trong trường hợp các cạnh song song, giữ lại cạnh có trọng số nhỏ nhất và xóa cạnh còn lại.

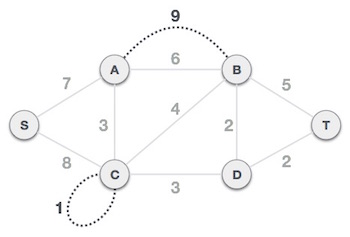
Bước 2: Chọn một nút bất kỳ để làm nút gốc

Giả sử chúng ta chọn nút S làm nút gốc với giải thuật Prim. Chúng ta có thể chọn tùy ý bất kỳ nút nào khác để làm nút gốc.

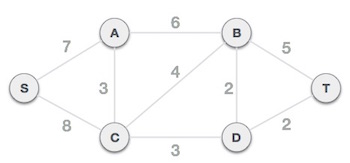
Bước 3: Kiểm tra các cạnh còn lại và chọn một cạnh có trọng số nhỏ nhất

Sau khi chọn nút gốc S, chúng ta thấy rằng SA và SC là hai cạnh có trọng số tương ứng là 7 và 8. Chúng ta chọn cạnh có trọng số nhỏ hơn là SA.

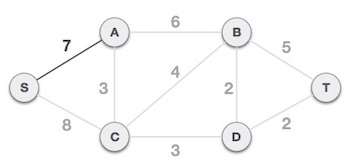
Bây giờ, cây S-7-A được xem như là một nút và chúng ta kiểm tra tất cả các cạnh còn lại bắt đầu từ nút này. Chúng ta tiếp tục chọn cạnh có trọng số nhỏ nhất và thêm nó vào trong cây.

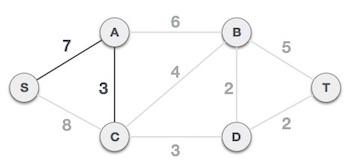
Sau bước này tạo nên cây S-7-A-3-C. Bây giờ chúng ta lại coi đó là một nút và kiểm tra tất cả các cạnh còn lại và sẽ chỉ chọn cạnh có trọng số nhỏ nhất. Trong ví dụ này là cạnh C-3-D có trọng số thấp nhất.

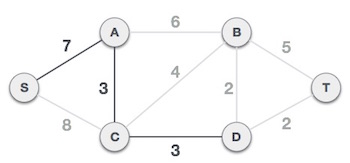
Sau khi thêm nút D vào cây khung, bây giờ chúng ta còn hai cạnh mà có cùng trọng số: D-2-T và D-2-B. Do đó chúng ta có thể thêm một trong hai cạnh. Tuy nhiên, bước tiếp theo sẽ lại thêm cạnh có trọng số 2 còn lại. Dưới đây là hình minh họa sau khi đã thêm hai cạnh.

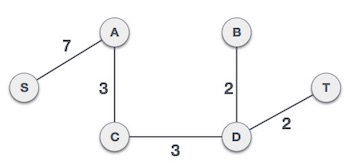
Từ ví dụ minh họa trên và ví dụ trong chương Giải thuật Kruskal: tìm cây khung nhỏ nhất, chúng ta thấy rằng cả hai ví dụ đều có chung kết quả dù cho sử dụng hai giải thuật khác nhau.