Giải thuật sắp xếp nhanh (Quick Sort)

Sắp xếp nhanh (Quick Sort) là gì ?

Giải thuật sắp xếp nhanh (Quick Sort) là một giải thuật hiệu quả cao và dựa trên việc chia mảng dữa liệu thành các mảng nhỏ hơn. Giải thuật sắp xếp nhanh chia mảng thành hai phần bằng cách so sánh từng phần tử của mảng với một phần tử được chọn gọi là phần tử chốt (Pivot): một mảng bao gồm các phần tử nhỏ hơn hoặc bằng phần tử chốt và mảng còn lại bao gồm các phần tử lớn hơn hoặc bằng phần tử chốt.

Tiến trình chia này diễn ra tiếp tục cho tới khi độ dài của các mảng con đều bằng 1. Giải thuật sắp xếp nhanh tỏ ra khá hiệu quả với các tập dữ liệu lớn khi mà độ phức tạp trường hợp trung bình và trường hợp xấu nhất là O(nlogn) với n là số phần tử.

Kỹ thuật chọn phần tử chốt trong giải thuật sắp xếp nhanh (Quick Sort)

Kỹ thuật chọn phần tử chốt ảnh hưởng khá nhiều đến khả năng rơi vào các vòng lặp vô hạn đối với các trường hợp đặc biệt. Tốt nhất là chọn phần tử chốt (pivot) nằm ở trung vị của danh sách. Khi đó, sau log₂(n) lần chia chúng ta sẽ đạt tới kích thước các mảng con bằng 1.

Dưới đây là các cách chọn phần tử chốt:

• Chọn phần tử đứng đầu hoặc đứng cuối làm phần tử chốt.
• Chọn phần tử đứng giữa danh sách làm phần tử chốt.
• Chọn phần tử trung vị trong ba phần tử đứng đầu, đứng giữa và đứng cuối làm phần tử chốt.
• Chọn phần tử ngẫu nhiên làm phần tử chốt. Tuy nhiên cách này rất dễ dẫn đến khả năng rơi vào các trường hợp đặc biệt.

Minh họa cách chia trong giải thuật sắp xếp nhanh (Quick Sort)

Hình minh họa dưới đây minh họa cách tìm phần tử chốt trong mảng. Ở đây, chúng ta chọn phần tử chốt đứng ở cuối danh sách.

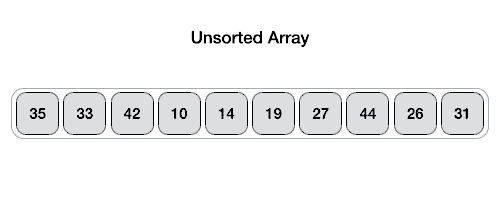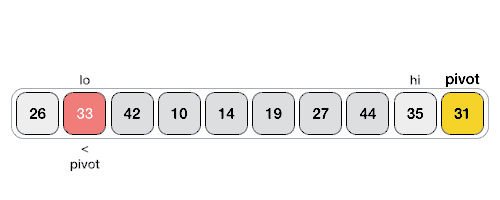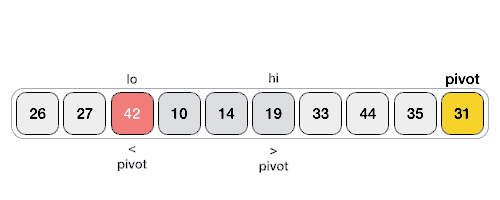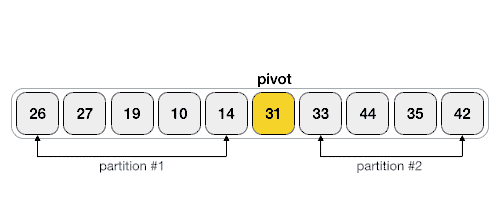
Phần tử chốt chia danh sách thành hai phần. Và sử dụng đệ qui, chúng ta tìm phần tử chốt cho các mảng con cho tới khi danh sách chỉ còn một phần tử.

Giải thuật phần tử chốt trong sắp xếp nhanh (Quick Sort)

Dựa vào cách chia danh sách trong giải thuật sắp xếp nhanh ở trên, chúng ta có thể viết một giải thuật như dưới đây.

<b>Bước 1</b>: Chọn phần tử chốt là phần tử có chỉ mục cao nhất (phần tử ở cuối danh sách)
<b>Bước 2</b>: Khai báo hai biến để trỏ tới bên trái và bên phải của danh sách, ngoại trừ phần tử chốt
<b>Bước 3</b>: Biến bên trái trỏ tới mảng con bên trái
<b>Bước 4</b>: Biến bên phải trỏ tới mảng con bên phải 
<b>Bước 5</b>: Khi giá trị tại biến bên trái là nhỏ hơn phần tử chốt thì di chuyển sang phải
<b>Bước 6</b>: Khi giá trị tại biến bên phải là lớn hơn phần tử chốt thì di chuyển sang trái 
<b>Bước 7</b>: Nếu không trong trường hợp cả bước 5 và bước 6 thì tráo đổi giá trị biến trái và phải
<b>Bước 8</b>: Nếu left ≥ right, thì đây chính là giá trị chốt mới

Giải thuật phần tử chốt mẫu trong sắp xếp nhanh (Quick Sort)

Từ các bước trên, chúng ta có thể suy ra code mẫu cho giải thuật sắp xếp nhanh (Quick Sort) như sau:

Bắt đầu hàm partitionFunc(left, right, pivot)
   leftPointer = left -1
   rightPointer = right

   while True thực hiện
      while A[++leftPointer] < pivot thực hiện
         //không làm điều gì            
      kết thúc while

      while rightPointer > 0 && A[--rightPointer] > pivot thực hiện
         //không làm điều gì     
      kết thúc while

      if leftPointer >= rightPointer
         break
      else                
         Tráo đổi leftPointer,rightPointer
      kết thúc if

   kết thúc while 

   Tráo đổi leftPointer,right
   return leftPointer

Kết thúc hàm

Giải thuật sắp xếp nhanh (Quick Sort)

Sử dụng giải thuật phần tử chốt một cách đệ qui, chúng ta có thể kết thúc với các mảng con nhỏ hơn. Sau đó mỗi mảng con này có thể được xử lý với sắp xếp nhanh. Dưới đây, mình sử dụng giải thuật đệ qui cho sắp xếp nhanh:

<b>Bước 1</b>: Lấy phần tử chốt là phần tử ở cuối danh sách
<b>Bước 2</b>: Chia mảng bởi sử dụng phần tử chốt
<b>Bước 3</b>: Sử dụng sắp xếp nhanh một cách đệ qui với mảng con bên trái 
<b>Bước 4</b>: Sử dụng sắp xếp nhanh một cách đệ qui với mảng con bên phải

Giải thuật mẫu cho Sắp xếp nhanh (Quick Sort)

Từ phần giải thuật trên, chúng ta có thể suy ra code mẫu cho giải thuật sử dụng đệ qui cho sắp xếp nhanh như sau:

Bắt đầu hàm quickSort(left, right)

   if right-left <= 0
      return
   else     
      pivot = A[right]
      partition = partitionFunc(left, right, pivot)
      quickSort(left,partition-1)
      quickSort(partition+1,right)    
   kết thúc if      

Kết thúc hàm