Sắp xếp nổi bọt (Bubble Sort) là gì ?
Sắp xếp nổi bọt là một giải thuật sắp xếp đơn giản. Giải thuật sắp xếp này được tiến hành dựa trên việc so sánh cặp phần tử liền kề nhau và tráo đổi thứ tự nếu chúng không theo thứ tự.
Giải thuật này không thích hợp sử dụng với các tập dữ liệu lớn khi mà độ phức tạp trường hợp xấu nhất và trường hợp trung bình là Ο(n2) với n là số phần tử.
Giải thuật sắp xếp nổi bọt là giải thuật chậm nhất trong số các giải thuật sắp xếp cơ bản. Giải thuật này còn chậm hơn giải thuật đổi chỗ trực tiếp mặc dù số lần so sánh bằng nhau, nhưng do đổi chỗ hai phần tử kề nhau nên số lần đổi chỗ nhiều hơn.
Cách giải thuật sắp xếp nổi bọt làm việc?
Giả sử chúng ta có một mảng không có thứ tự gồm các phần tử như dưới đây. Bây giờ chúng ta sử dụng giải thuật sắp xếp nổi bọt để sắp xếp mảng này.

Giải thuật sắp xếp nổi bọt bắt đầu với hai phần tử đầu tiên, so sánh chúng để kiểm tra xem phần tử nào lớn hơn.

Trong trường hợp này, 33 lớn hơn 14, do đó hai phần tử này đã theo thứ tự. Tiếp đó chúng ta so sánh 33 và 27.

Chúng ta thấy rằng 33 lớn hơn 27, do đó hai giá trị này cần được tráo đổi thứ tự.
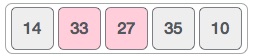
Mảng mới thu được sẽ như sau:

Tiếp đó chúng ta so sánh 33 và 35. Hai giá trị này đã theo thứ tự.

Sau đó chúng ta so sánh hai giá trị kế tiếp là 35 và 10.

Vì 10 nhỏ hơn 35 nên hai giá trị này chưa theo thứ tự.

Tráo đổi thứ tự hai giá trị. Chúng ta đã tiến tới cuối mảng. Vậy là sau một vòng lặp, mảng sẽ trông như sau:

Để đơn giản, tiếp theo mình sẽ hiển thị hình ảnh của mảng sau từng vòng lặp. Sau lần lặp thứ hai, mảng sẽ trông giống như:

Sau mỗi vòng lặp, ít nhất một giá trị sẽ di chuyển tới vị trí cuối. Sau vòng lặp thứ 3, mảng sẽ trông giống như:
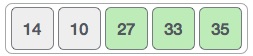
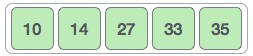
Và khi không cần tráo đổi thứ tự phần tử nào nữa, giải thuật sắp xếp nổi bọt thấy rằng mảng đã được sắp xếp xong.
Tiếp theo, chúng ta tìm hiểu thêm một số khía cạnh thực tế của giải thuật sắp xếp.
Giải thuật cho sắp xếp nổi bọt (Bubble Sort)
Giả sử list là một mảng có n phần tử. Tiếp đó giả sử hàm swap để tráo đổi giá trị của các phần tử trong mảng (đây là giả sử, tất nhiên là bạn có thể viết code riêng cho hàm swap này).
Bắt đầu giải thuật BubbleSort(list)
for tất cả phần tử trong list
if list[i] > list[i+1]
swap(list[i], list[i+1])
kết thúc if
kết thúc for
return list
Kết thúc BubbleSort
Giải thuật mẫu cho sắp xếp nổi bọt (Bubble Sort)
Chúng ta thấy rằng giải thuật sắp xếp nổi bọt so sánh mỗi cặp phần tử trong mảng trừ khi cả toàn bộ mảng đó đã hoàn toàn được sắp xếp theo thứ tự tăng dần. Điều này có thể làm tăng độ phức tạp, tức là tăng các thao tác so sánh và tráo đổi không cần thiết nếu như mảng này không cần sự tráo đổi nào nữa khi tất cả các phần tử đã được sắp xếp theo thứ tự tăng dần rồi.
Để tránh việc này xảy ra, chúng ta có thể sử dụng một biến swapped chẳng hạn để giúp chúng ta biết có cần thực hiện thao tác tráo đổi thứ tự hay không. Nếu không cần thiết thì thoát khỏi vòng lặp.
Bạn theo dõi phần giải thuật mẫu minh họa sau:
Bắt đầu hàm bubbleSort( list : mảng các phần tử )
loop = list.count;
for i = 0 tới loop-1 thực hiện:
swapped = false
for j = 0 tới loop-1 thực hiện:
/* so sánh các phần tử cạnh nhau */
if list[j] > list[j+1] then
/* tráo đổi chúng */
swap( list[j], list[j+1] )
swapped = true
kết thúc if
kết thúc for
/*Nếu không cần tráo đổi phần tử nào nữa thì
tức là mảng đã được sắp xếp. Thoát khỏi vòng lặp.*/
if(not swapped) then
break
kết thúc if
kết thúc for
Kết thúc hàm return list
Triển khai giải thuật sắp xếp nổi bọt trong C
Một điều nữa mà chúng ta chưa nói tới trong 2 phần thiết kế giải thuật đó là cứ sau mỗi vòng lặp thì các giá trị lớn nhất sẽ xuất hiện ở vị trí cuối mảng (như trong hình minh họa: sau vòng lặp 1 là 35; sau vòng lặp 2 là 33 và 35; …). Do đó, vòng lặp tiếp theo sẽ không cần bao gồm cả các phần tử đã được sắp xếp này. Để thực hiện điều này, trong phần code chúng ta giới hạn vòng lặp lặp bên để tránh phải lặp lại các giá trị đã qua sắp xếp này.






















Unpublished comment
Viết câu trả lời