Giải thuật tìm kiếm theo chiều rộng

Giải thuật tìm kiếm theo chiều rộng là gì ?

Giải thuật tìm kiếm theo chiều rộng (Breadth First Search – viết tắt là BFS) duyệt qua một đồ thị theo chiều rộng và sử dụng hàng đợi (queue) để ghi nhớ đỉnh liền kề để bắt đầu việc tìm kiếm khi không gặp được đỉnh liền kề trong bất kỳ vòng lặp nào.

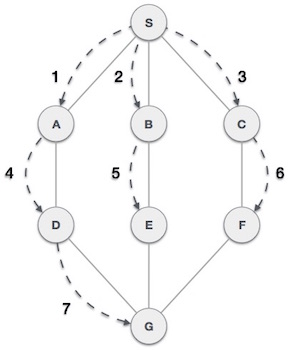
Như trong hình ví dụ trên, giải thuật tìm kiếm theo chiều rộng duyệt từ A tới B tới E tới F sau đó tới C, tới G và cuối cùng tới D. Giải thuật này tuân theo qui tắc:

• Qui tắc 1: Duyệt tiếp tới đỉnh liền kề mà chưa được duyệt. Đánh dấu đỉnh mà đã được duyệt. Hiển thị đỉnh đó và đẩy vào trong một hàng đợi (queue)..
• Qui tắc 2: Nếu không tìm thấy đỉnh liền kề, thì xóa đỉnh đầu tiên trong hàng đợi.
• Qui tắc 3: Lặp lại Qui tắc 1 và 2 cho tới khi hàng đợi là trống.

Bảng dưới đây minh họa cách giải thuật tìm kiếm theo chiều rộng làm việc với một ví dụ đơn giản sau:

Bước	Duyệt	Miêu tả
1.		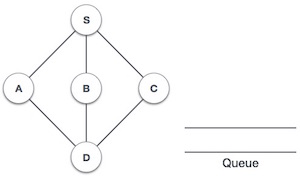Khởi tạo hàng đợi (queue)
2.		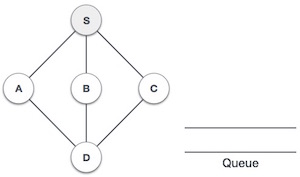Chúng ta bắt đầu duyệt đỉnh S (đỉnh bắt đầu) và đánh dấu đỉnh này là đã duyệt.
3.		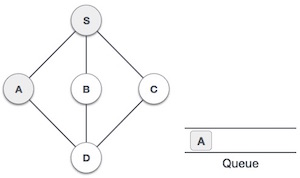Sau đó chúng ta tìm đỉnh liền kề với Smà chưa được duyệt. Trong ví dụ này chúng ta có 3 đỉnh, và theo thứ tự chữ cái chúng ta chọn đỉnh A đánh dấu là đã duyệt và xếp A vào hàng đợi.
4.		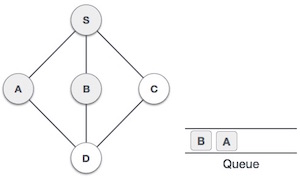Tiếp tục duyệt đỉnh liền kề với S là B. Đánh dấu là đã duyệt và xếp đỉnh này vào hàng đợi.
5.		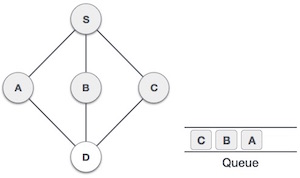Tiếp tục duyệt đỉnh liền kề với S là C. Đánh dấu là đã duyệt và xếp đỉnh này vào hàng đợi.
6.		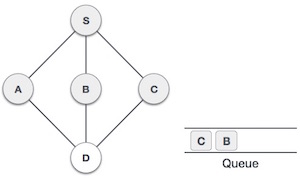Bây giờ đỉnh S không còn đỉnh nào liền kề mà chưa được duyệt. Bây giờ chúng ta rút A từ hàng đợi.
7.		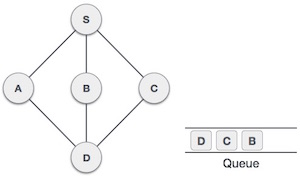Từ đỉnh A chúng ta có đỉnh liền kề là D và là đỉnh chưa được duyệt. Đánh dấu đỉnh D là đã duyệt và xếp vào hàng đợi.

Đến đây, chúng ta thấy rằng không còn đỉnh nào là chưa được đánh dấu (chưa được duyệt với ví dụ trong bảng này). Nhưng giải thuật vẫn tiếp tục, chúng ta vẫn tiếp tục rút các đỉnh từ hàng đợi theo thứ tự để tìm tất cả các đỉnh mà chưa được duyệt. Khi hàng đợi là trống thì đó là lúc kết thúc giải thuật.

Ví dụ Tìm kiếm theo chiều rộng trong C

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAX 5

struct Vertex {
   char label;
   bool visited;
};

//khai bao cac bien cho hang doi (queue)

int queue[MAX];
int rear = -1;
int front = 0;
int queueItemCount = 0;

//khai bao cac bien cho do thi (graph)

//khai bao danh sach cac dinh (vertex)
struct Vertex* lstVertices[MAX];

//khai bao mot ma tran ke (adjacency matrix)
int adjMatrix[MAX][MAX];

//mot bien de dem so dinh (vertex)
int vertexCount = 0;

//cac ham thao tac tren hang doi (queue)

void insert(int data) {
   queue[++rear] = data;
   queueItemCount++;
}

int removeData() {
   queueItemCount--;
   return queue[front++]; 
}

bool isQueueEmpty() {
   return queueItemCount == 0;
}

//cac ham thao tac tren do thi (graph)

//them dinh vao danh sach cac dinh
void addVertex(char label) {
   struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}

//them canh vao mang cac canh
void addEdge(int start,int end) {
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

//hien thi cac dinh
void displayVertex(int vertexIndex) {
   printf("%c ",lstVertices[vertexIndex]->label);
}       

//lay dinh chua duyet tu ma tran ke
int getAdjUnvisitedVertex(int vertexIndex) {
   int i;

   for(i = 0; i<vertexCount; i++) {
      if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false)
         return i;
   }

   return -1;
}

void breadthFirstSearch() {
   int i;

   //danh dau nut dau tien (first node) la da duyet (visited)
   lstVertices[0]->visited = true;

   //hien thi dinh
   displayVertex(0);   

   //chen chi muc cua dinh vao trong hang doi
   insert(0);
   int unvisitedVertex;

   while(!isQueueEmpty()) {
      //Rut dinh chua duoc duyet tu hang doi
      int tempVertex = removeData();   

      //khong tim thay dinh lien ke
      while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {    
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         insert(unvisitedVertex);               
      }

   }   

   //hang doi la trong, hoan thanh tim kiem, reset gia tri cua visited        
   for(i = 0;i<vertexCount;i++) {
      lstVertices[i]->visited = false;
   }    
}

int main() {
   int i, j;

   for(i = 0; i<MAX; i++) { // thiet lap cac gia tri
      for(j = 0; j<MAX; j++) // cua ma tran ke la 0
         adjMatrix[i][j] = 0;
   }

   addVertex('S');   // 0
   addVertex('A');   // 1
   addVertex('B');   // 2
   addVertex('C');   // 3
   addVertex('D');   // 4

   addEdge(0, 1);    // S - A
   addEdge(0, 2);    // S - B
   addEdge(0, 3);    // S - C
   addEdge(1, 4);    // A - D
   addEdge(2, 4);    // B - D
   addEdge(3, 4);    // C - D

   printf("\nTim kiem theo chieu rong: ");

   breadthFirstSearch();

   return 0;
}

Kết quả

Biên dịch và chạy chương trình C trên sẽ cho kết quả: