Chương trước chúng ta đã cùng tìm hiểu về phân tích lý thuyết và một số khái niệm về độ phức tạp thời gian và độ phức tạp bộ nhớ trong phân tích giải thuật. Chương này mình sẽ trình bày về Phân tích tiệm cận trong Cấu trúc dữ liệu và Giải thuật.
Phân tích tiệm cận là gì ?
Phân tích tiệm cận của một giải thuật là khái niệm giúp chúng ta ước lượng được thời gian chạy (Running Time) của một giải thuật. Sử dụng phân tích tiệm cận, chúng ta có thể đưa ra kết luận tốt nhất về các tình huống trường hợp tốt nhất, trường hợp trung bình, trường hợp xấu nhất của một giải thuật. Để tham khảo về các trường hợp này, bạn có thể tìm hiểu chương Cấu trúc dữ liệu là gì ?.
Phân tích tiệm cận tức là tiệm cận dữ liệu đầu vào (Input), tức là nếu giải thuật không có Input thì kết luận cuỗi cùng sẽ là giải thuật sẽ chạy trong một lượng thời gian cụ thể và là hằng số. Ngoài nhân tố Input, các nhân tố khác được xem như là không đổi.
Phân tích tiệm cận nói đến việc ước lượng thời gian chạy của bất kỳ phép tính nào trong các bước tính toán. Ví dụ, thời gian chạy của một phép tính nào đó được ước lượng là một hàm f(n) và với một phép tính khác là hàm g(n<sup>2</sup>). Điều này có nghĩa là thời gian chạy của phép tính đầu tiên sẽ tăng tuyến tính với sự tăng lên của n và thời gian chạy của phép tính thứ hai sẽ tăng theo hàm mũ khi n tăng lên. Tương tự, khi n là khá nhỏ thì thời gian chạy của hai phép tính là gần như nhau.
Thường thì thời gian cần thiết bởi một giải thuật được chia thành 3 loại:
- Trường hợp tốt nhất: là thời gian nhỏ nhất cần thiết để thực thi chương trình.
- Trường hợp trung bình: là thời gian trung bình cần thiết để thực thi chương trình.
- Trường hợp xấu nhất: là thời gian tối đa cần thiết để thực thi chương trình.
Asymptotic Notation trong Cấu trúc dữ liệu và giải thuật
Dưới đây là các Asymptotic Notation được sử dụng phổ biến trong việc ước lượng độ phức tạp thời gian chạy của một giải thuật:
- Ο Notation
- Ω Notation
- θ Notation
Big Oh Notation, Ο trong Cấu trúc dữ liệu và giải thuật
Ο(n) là một cách để biểu diễn tiệm cận trên của thời gian chạy của một thuật toán. Nó ước lượng độ phức tạp thời gian trường hợp xấu nhất hay chính là lượng thời gian dài nhất cần thiết bởi một giải thuật (thực thi từ bắt đầu cho đến khi kết thúc). Đồ thị biểu diễn như sau:
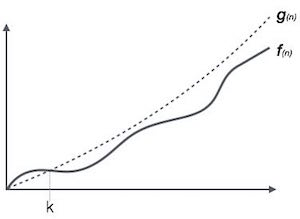
Ví dụ, gọi f(n) và g(n) là các hàm không giảm định nghĩa trên các số nguyên dương (tất cả các hàm thời gian đều thỏa mãn các điều kiện này):
Ο(<i>f</i>(n)) = { <i>g</i>(n) : nếu tồn tại c > 0 và n<sub>0</sub> sao cho <i>g</i>(n) ≤ c.<i>f</i>(n) với mọi n > n<sub>0</sub>. }Omega Notation, Ω trong Cấu trúc dữ liệu và giải thuật
The Ω(n) là một cách để biểu diễn tiệm cận dưới của thời gian chạy của một giải thuật. Nó ước lượng độ phức tạp thời gian trường hợp tốt nhất hay chính là lượng thời gian ngắn nhất cần thiết bởi một giải thuật. Đồ thị biểu diễn như sau:
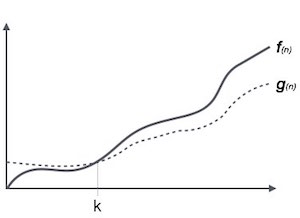
Ví dụ, với một hàm f(n):
Ω(<i>f</i>(n)) ≥ { <i>g</i>(n) : nếu tồn tại c > 0 và n<sub>0</sub> sao cho <i>g</i>(n) ≤ c.<i>f</i>(n) với mọi n > n<sub>0</sub>. }
Theta Notation, θ trong Cấu trúc dữ liệu và giải thuật
The θ(n) là cách để biểu diễn cả tiệm cận trên và tiệm cận dưới của thời gian chạy của một giải thuật. Bạn nhìn vào đồ thì sau:
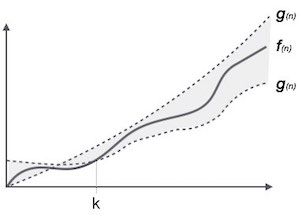
θ(<i>f</i>(n)) = { <i>g</i>(n) nếu và chỉ nếu <i>g</i>(n) = Ο(<i>f</i>(n)) và <i>g</i>(n) = Ω(<i>f</i>(n)) với mọi n > n<sub>0</sub>. }
Một số Asymptotic Notation phổ biến trong cấu trúc dữ liệu và giải thuật
| hằng số | − | Ο(1) |
| logarit | − | Ο(log n) |
| Tuyến tính (Linear) | − | Ο(n) |
| n log n | − | Ο(n log n) |
| Bậc hai (Quadratic) | − | Ο(n2) |
| Bậc 3 (cubic) | − | Ο(n3) |
| Đa thức (polynomial) | − | nΟ(1) |
| Hàm mũ (exponential) | − | 2Ο(n) |






















Unpublished comment
Viết câu trả lời